Random Numbers with the STM32F4
I’ve been looking at the RTP specification lately and it’s hard not to notice the protocol’s reliance on random numbers. For instance, the RFC recommends the following should be generated randomly:
- SSRC
- initial sequence number
- initial timestamp value
- RTCP transmission interval
The rationale for why these values should be random doesn’t really apply to my intended use case of RTP so I was prepared to ignore it. However the STM32F407 microcontroller I was using features a True Random Number Generator, so I thought I might as well put it to good use.
Determining How Random
I wanted to conduct some basic sanity checking on the randomness of the output from the TRNG. This, it turns out, isn’t a particularly trivial task. Rather than attempt to implement the necessary statistical methods myself, I went Googling for some existing programs and found this list.
I initially tried using the NIST STS test suite but found it had a somewhat clunky interface, and correctly using it would likely require more time than I was prepared to give. Additionally, ST have already produced an application note on testing a STM32 against the NIST STS test suite - “AN4230 Application note” (June 2016 DocID024118 Rev 2).
Moving onto the other listed programs I eventually settled on using the PractRand and dieharder test suites. Both of these were written to test RNGs, and it’s recommended to provide each with a stream of random numbers rather than a saved file. UDP seemed as good a method as any to export the random numbers from the STM32 to a computer.
Test Setup
All STM32 source code and Python utility files can be found in the following github repository in the directory test/true_random_number_generator as of the tag TEST_TRNG_1.
The following diagram presents a rough overview of the software involved in testing the TRNG:
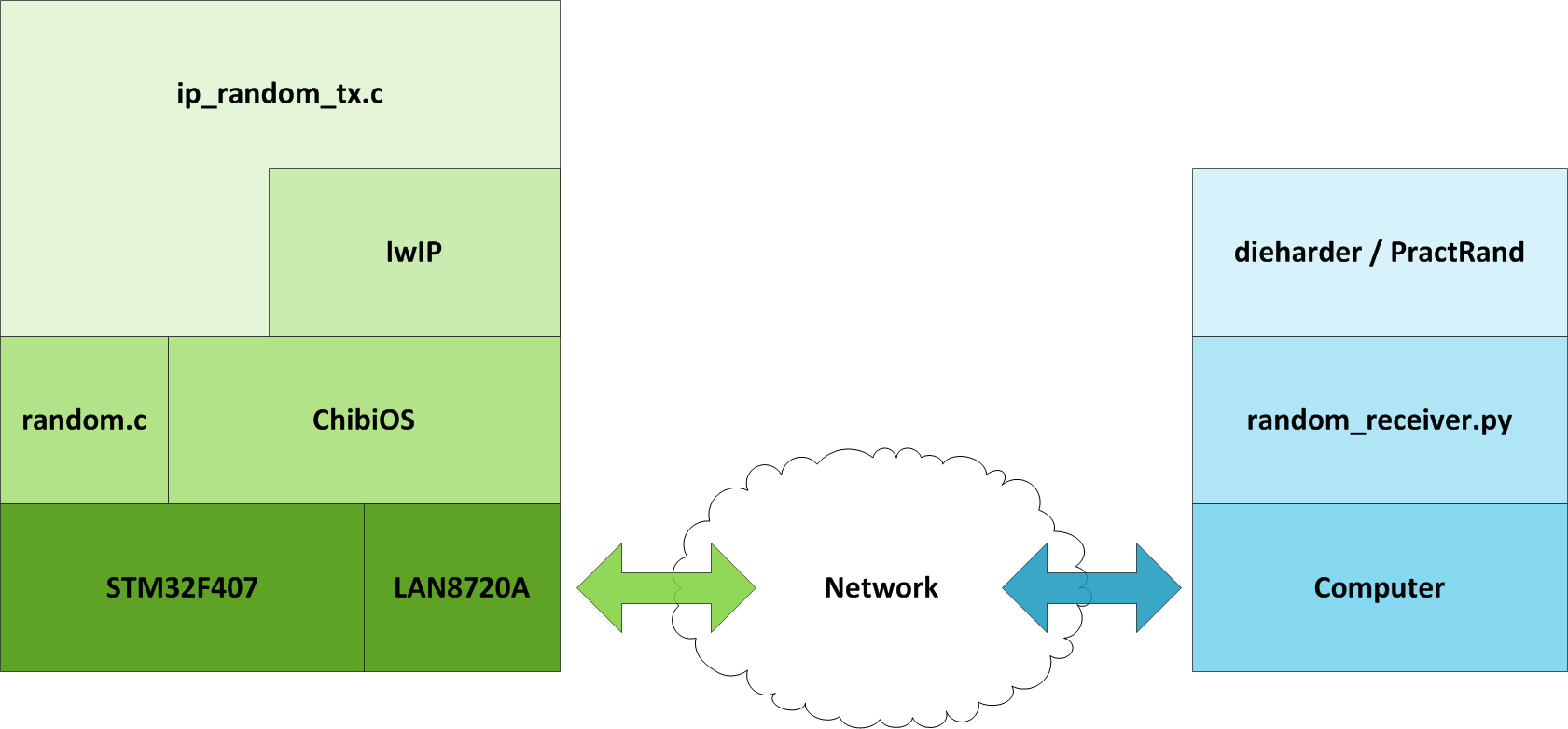
STM32 Code
The code is targeted for the following hardware:
- STM32F4DISCOVERY
- STM32F4DIS-EXT (LAN8720A Ethernet PHY used to transfer random numbers to a computer. UART or maybe USB could be instead)
The IP address of the MCU and remote PC are statically assigned, in the file: src/project.h.
The file: src/ip_random_tx.c handles the UDP/IP transmission, where an infinite loop:
- Allocates an LWIP netbuf of 1460 bytes
- Fills the buffer by calling into
src/random.cto read from theRNG_DRregister 365 times - Transmits the UDP message to the target IP/UDP port
- Deletes the netbuf
utils/random_receiver.py
This script acts a UDP listener for the random data stream transmitted by the STM32F407. It simply dumps out the random payload over stdout so it can easily be piped into dieharder or PractRand.
The script can be run with --help to list the possible command line arguments, and examples of the commands used are included below with the results.
Measuring Throughput
The RM0090 Reference Manual (DocID018909 Rev 7) states the RNG requires:
40 periods of the PLL48CLK clock signal between two consecutive random numbers
This gives a theoretical throughput of:
(48,000,000 / 40) * 4 * 8 = 38.40 Mb/s
From a Wireshark capture I was able to see that the STM32F4 was transmitting a fairly consistent 2353 packets per second. Since these contain a payload of 365 32-bit samples this gives the actual throughput to be:
2353 * 365 * 4 * 8 = 27.48 Mb/s
The mutex protecting the RNG register does significant damage to the recorded throughput, and if removed (safe if only one thread ever calls randomGet()) then packets per second increases to approximately 2832 or:
2832 * 365 * 4 * 8 = 33.08 Mb/s
Testing Summary
The full suite of default dieharder tests took approximately 20 hours to complete. During which time over 256.4 GB of random numbers were transferred.
The only concerns flagged during the run were two tests which were classified as weak.
After skimming over the man page it is apparently quite normal to have several tests be identified as such. The man page of dieharder can be found online, or in the following location of the built source:
man dieharder/dieharder.1
PractRand was left to run for 24 hours over which time approximately 287.5 GB were transmitted. During the course of testing, 4 tests were reported as having “unusual” results. Again, I don’t think this is a massive cause for concern (where a status of “fail” would be). To note, testing 287.5 GB is perhaps a little on the stingy side (1 TiB seems to be a recommended input size), but a runtime of 24 hours was long enough for me.
The full output of dieharder and PractRand results are available below.
Somewhat unsurprisingly, I am confident that the TRNG produces sufficiently random numbers (for my intended purpose at least). However it’s worth throwing in an…
Aside on Security
First and foremost I have not done any serious work in the security/cryptography domain, but the recommended advice as far as random numbers are it’s safer to combine the output of several sources of random numbers than to completely trust anyone. This is for example what the Linux kernel does (which CloudFlare also has an article on).
Unfortunately for embedded systems finding other good sources of randomness can be pretty difficult.
Why are random numbers so important in cryptography?
First and foremost we want to be using passwords/encryption keys which are hard to guess. Since no person really wants the job of throwing some dice every time secrecy is desired, we need to rely on using a source(s) of randomness to achieve this.
How can a message be decrypted by a recipient if it was encrypted with a randomly generated key?
The answer to this is a little more complicated that I first realised, as it depends on what type of encryption is being used:
-
Asymmetric key encryption - A public/private key pair is created by initially generating a large, random number and then employing some clever math. The public key can be used to encrypt data, which only the private key can decrypt. As long as the private key is kept safe it therefore does not matter if a third party has a copy of the public key, or eavesdrops on the encrypted message. Asymmetric key encryption is more CPU intensive than symmetric key encryption.
-
Symmetric key encryption - A single encryption key /“shared secret” is used by a cipher for both encryption and decryption of a message. This secret may be randomly generated or come from user input. The only way a message encrypted with a symmetric key should be able to be decrypted is by someone who knows the secret key. This leads to the related problem of key distribution. We need to safely transmit the encryption key to the intended recipient while also keeping it safe from an eavesdropper.
Considering a simplified overview of how HTTPS works, we see that both asymmetric and symmetric key encryption are employed each time you connect to a secure website. Furthermore there are two examples of when random numbers are used to facilitate encryption.
- The client acquires the server’s public key (which was generated using random numbers sometime in the past).
- The client generates a random string to use as the “premaster secret”.
- The client uses the server’s public key to encrypt the premaster secret before transmitting it to the server.
- The server and client now calculate a “master secret” based on the premaster secret which they will use for symmetric encryption of the session.
The First Few Milliseconds of a HTTPS Connection is a more detailed dissection of the HTTPS connection handshake.
Building Test Programs from Source
Below are the commands I used to build the packages from source. I can’t guarantee what existing packages I already had installed on my system (Debian 8 / Jessie) which may have met dependencies for these packages.
At the very least, some of the packages included with build-essential are required:
sudo apt-get install build-essential
Dieharder
Build
sudo apt-get install libgsl0-dev
wget https://www.phy.duke.edu/~rgb/General/dieharder/dieharder-3.31.1.tgz
tar -vxf dieharder-3.31.1.tgz
cd dieharder-3.31.1
#
# The following command may need to be issued if you
# get the following at the make stage:
# mv: cannot stat ‘.deps/libdieharder_la-bits.Tpo’: No such file or directory
#
# autoreconf -i
./autogen.sh
make
Stdin Usage Example
cat /dev/urandom | ./dieharder/dieharder -a -g 200
-
-a runs all the tests with standard/default options to create a report.
-
-g 200 selects generator 200 for testing, reading raw binary from stdin
PractRand
Build
wget http://downloads.sourceforge.net/project/pracrand/PractRand_0.93.zip
unzip PractRand_0.93.zip -d PractRand
cd PractRand
g++ -c src/*.cpp src/RNGs/*.cpp src/RNGs/other/*.cpp -O3 -Iinclude -pthread
ar rcs libPractRand.a *.o
rm *.o
g++ -std=c++11 -o RNG_test tools/RNG_test.cpp libPractRand.a -O3 -Iinclude -pthread
g++ -o RNG_benchmark tools/RNG_benchmark.cpp libPractRand.a -O3 -Iinclude -pthread
g++ -o RNG_output tools/RNG_output.cpp libPractRand.a -O3 -Iinclude -pthread
Stdin Usage Example
cat /dev/urandom | ./PractRand/RNG_test stdin
- stdin Use stdin as an RNG name to allow piping random numbers.
STS
Build
wget http://csrc.nist.gov/groups/ST/toolkit/rng/documents/sts-2.1.2.zip
unzip sts-2.1.2.zip
cd sts-2.1.2/sts-2.1.2
make
Full Results
Dieharder
Invoked with:
./random_receiver.py --local-ip 192.168.1.154 --local-port 50002 | ~/random/dieharder/dieharder-3.31.1/dieharder/dieharder -a -g 200
Output:
#=============================================================================#
# dieharder version 3.31.1 Copyright 2003 Robert G. Brown #
#=============================================================================#
rng_name |rands/second| Seed |
stdin_input_raw| 8.59e+05 | 713411196|
#=============================================================================#
test_name |ntup| tsamples |psamples| p-value |Assessment
#=============================================================================#
diehard_birthdays| 0| 100| 100|0.83540526| PASSED
diehard_operm5| 0| 1000000| 100|0.04466247| PASSED
diehard_rank_32x32| 0| 40000| 100|0.84345278| PASSED
diehard_rank_6x8| 0| 100000| 100|0.93010893| PASSED
diehard_bitstream| 0| 2097152| 100|0.81511448| PASSED
diehard_opso| 0| 2097152| 100|0.60244761| PASSED
diehard_oqso| 0| 2097152| 100|0.29607203| PASSED
diehard_dna| 0| 2097152| 100|0.94207248| PASSED
diehard_count_1s_str| 0| 256000| 100|0.17214439| PASSED
diehard_count_1s_byt| 0| 256000| 100|0.52693251| PASSED
diehard_parking_lot| 0| 12000| 100|0.49340705| PASSED
diehard_2dsphere| 2| 8000| 100|0.63351978| PASSED
diehard_3dsphere| 3| 4000| 100|0.88070467| PASSED
diehard_squeeze| 0| 100000| 100|0.68528643| PASSED
diehard_sums| 0| 100| 100|0.48200105| PASSED
diehard_runs| 0| 100000| 100|0.92395165| PASSED
diehard_runs| 0| 100000| 100|0.32025457| PASSED
diehard_craps| 0| 200000| 100|0.79845431| PASSED
diehard_craps| 0| 200000| 100|0.05912745| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.03563616| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.53772173| PASSED
sts_monobit| 1| 100000| 100|0.13457942| PASSED
sts_runs| 2| 100000| 100|0.05028770| PASSED
sts_serial| 1| 100000| 100|0.18837197| PASSED
sts_serial| 2| 100000| 100|0.62362568| PASSED
sts_serial| 3| 100000| 100|0.96394260| PASSED
sts_serial| 3| 100000| 100|0.98611130| PASSED
sts_serial| 4| 100000| 100|0.97441310| PASSED
sts_serial| 4| 100000| 100|0.50273335| PASSED
sts_serial| 5| 100000| 100|0.95235380| PASSED
sts_serial| 5| 100000| 100|0.73830497| PASSED
sts_serial| 6| 100000| 100|0.08727008| PASSED
sts_serial| 6| 100000| 100|0.55263697| PASSED
sts_serial| 7| 100000| 100|0.26199891| PASSED
sts_serial| 7| 100000| 100|0.64351336| PASSED
sts_serial| 8| 100000| 100|0.17155686| PASSED
sts_serial| 8| 100000| 100|0.28361213| PASSED
sts_serial| 9| 100000| 100|0.24682859| PASSED
sts_serial| 9| 100000| 100|0.61277945| PASSED
sts_serial| 10| 100000| 100|0.12638033| PASSED
sts_serial| 10| 100000| 100|0.04882949| PASSED
sts_serial| 11| 100000| 100|0.81989820| PASSED
sts_serial| 11| 100000| 100|0.71687818| PASSED
sts_serial| 12| 100000| 100|0.84325914| PASSED
sts_serial| 12| 100000| 100|0.29387487| PASSED
sts_serial| 13| 100000| 100|0.52245839| PASSED
sts_serial| 13| 100000| 100|0.20404980| PASSED
sts_serial| 14| 100000| 100|0.48662144| PASSED
sts_serial| 14| 100000| 100|0.48048911| PASSED
sts_serial| 15| 100000| 100|0.95237164| PASSED
sts_serial| 15| 100000| 100|0.92841465| PASSED
sts_serial| 16| 100000| 100|0.78201956| PASSED
sts_serial| 16| 100000| 100|0.83320012| PASSED
rgb_bitdist| 1| 100000| 100|0.81515862| PASSED
rgb_bitdist| 2| 100000| 100|0.93546761| PASSED
rgb_bitdist| 3| 100000| 100|0.23672512| PASSED
rgb_bitdist| 4| 100000| 100|0.90336199| PASSED
rgb_bitdist| 5| 100000| 100|0.99516746| WEAK
rgb_bitdist| 6| 100000| 100|0.16042521| PASSED
rgb_bitdist| 7| 100000| 100|0.44818292| PASSED
rgb_bitdist| 8| 100000| 100|0.89829027| PASSED
rgb_bitdist| 9| 100000| 100|0.43722681| PASSED
rgb_bitdist| 10| 100000| 100|0.07995763| PASSED
rgb_bitdist| 11| 100000| 100|0.43174508| PASSED
rgb_bitdist| 12| 100000| 100|0.28906516| PASSED
rgb_minimum_distance| 2| 10000| 1000|0.29850666| PASSED
rgb_minimum_distance| 3| 10000| 1000|0.47989334| PASSED
rgb_minimum_distance| 4| 10000| 1000|0.76601854| PASSED
rgb_minimum_distance| 5| 10000| 1000|0.28904194| PASSED
rgb_permutations| 2| 100000| 100|0.99038654| PASSED
rgb_permutations| 3| 100000| 100|0.45475456| PASSED
rgb_permutations| 4| 100000| 100|0.78768172| PASSED
rgb_permutations| 5| 100000| 100|0.14063439| PASSED
rgb_lagged_sum| 0| 1000000| 100|0.84286997| PASSED
rgb_lagged_sum| 1| 1000000| 100|0.28915502| PASSED
rgb_lagged_sum| 2| 1000000| 100|0.76418500| PASSED
rgb_lagged_sum| 3| 1000000| 100|0.94152242| PASSED
rgb_lagged_sum| 4| 1000000| 100|0.79196027| PASSED
rgb_lagged_sum| 5| 1000000| 100|0.96621927| PASSED
rgb_lagged_sum| 6| 1000000| 100|0.08385351| PASSED
rgb_lagged_sum| 7| 1000000| 100|0.69553029| PASSED
rgb_lagged_sum| 8| 1000000| 100|0.26662831| PASSED
rgb_lagged_sum| 9| 1000000| 100|0.14516487| PASSED
rgb_lagged_sum| 10| 1000000| 100|0.52098361| PASSED
rgb_lagged_sum| 11| 1000000| 100|0.79708332| PASSED
rgb_lagged_sum| 12| 1000000| 100|0.82042220| PASSED
rgb_lagged_sum| 13| 1000000| 100|0.62178217| PASSED
rgb_lagged_sum| 14| 1000000| 100|0.48726412| PASSED
rgb_lagged_sum| 15| 1000000| 100|0.88369110| PASSED
rgb_lagged_sum| 16| 1000000| 100|0.18805319| PASSED
rgb_lagged_sum| 17| 1000000| 100|0.95238577| PASSED
rgb_lagged_sum| 18| 1000000| 100|0.51863217| PASSED
rgb_lagged_sum| 19| 1000000| 100|0.34248853| PASSED
rgb_lagged_sum| 20| 1000000| 100|0.32212559| PASSED
rgb_lagged_sum| 21| 1000000| 100|0.60051529| PASSED
rgb_lagged_sum| 22| 1000000| 100|0.67338389| PASSED
rgb_lagged_sum| 23| 1000000| 100|0.91690604| PASSED
rgb_lagged_sum| 24| 1000000| 100|0.72290954| PASSED
rgb_lagged_sum| 25| 1000000| 100|0.58708112| PASSED
rgb_lagged_sum| 26| 1000000| 100|0.46429208| PASSED
rgb_lagged_sum| 27| 1000000| 100|0.99972001| WEAK
rgb_lagged_sum| 28| 1000000| 100|0.55150125| PASSED
rgb_lagged_sum| 29| 1000000| 100|0.73345844| PASSED
rgb_lagged_sum| 30| 1000000| 100|0.55925322| PASSED
rgb_lagged_sum| 31| 1000000| 100|0.81852547| PASSED
rgb_lagged_sum| 32| 1000000| 100|0.65610325| PASSED
rgb_kstest_test| 0| 10000| 1000|0.14108036| PASSED
dab_bytedistrib| 0| 51200000| 1|0.42264375| PASSED
dab_dct| 256| 50000| 1|0.41282572| PASSED
Preparing to run test 207. ntuple = 0
dab_filltree| 32| 15000000| 1|0.86164663| PASSED
dab_filltree| 32| 15000000| 1|0.27706344| PASSED
Preparing to run test 208. ntuple = 0
dab_filltree2| 0| 5000000| 1|0.04548537| PASSED
dab_filltree2| 1| 5000000| 1|0.89796302| PASSED
Preparing to run test 209. ntuple = 0
dab_monobit2| 12| 65000000| 1|0.18208275| PASSED
With the output from random_receiver.py being:
############################
Duration (s): 72176.53291201591
Packets Rx: 168800068
Bytes Rx (B): 246448099280
PractRand
Invoked with:
./random_receiver.py --local-ip 192.168.1.154 --local-port 50002 | ~/random/PractRand/RNG_test stdin -tlmax 24h
Output:
RNG_test using PractRand version 0.93
RNG = RNG_stdin, seed = 0x5a46a561
test set = normal, folding = standard(unknown format)
rng=RNG_stdin, seed=0x5a46a561
length= 8 megabytes (2^23 bytes), time= 2.5 seconds
no anomalies in 107 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 16 megabytes (2^24 bytes), time= 5.6 seconds
no anomalies in 119 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 32 megabytes (2^25 bytes), time= 11.2 seconds
no anomalies in 130 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 64 megabytes (2^26 bytes), time= 22.0 seconds
no anomalies in 139 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 128 megabytes (2^27 bytes), time= 42.8 seconds
Test Name Raw Processed Evaluation
[Low1/8]FPF-14+6/16:all R= +4.7 p = 7.2e-4 unusual
...and 150 test result(s) without anomalies
rng=RNG_stdin, seed=0x5a46a561
length= 256 megabytes (2^28 bytes), time= 83.8 seconds
no anomalies in 162 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 512 megabytes (2^29 bytes), time= 165 seconds
no anomalies in 171 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 1 gigabyte (2^30 bytes), time= 327 seconds
no anomalies in 183 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 2 gigabytes (2^31 bytes), time= 651 seconds
no anomalies in 194 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 4 gigabytes (2^32 bytes), time= 1297 seconds
no anomalies in 203 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 8 gigabytes (2^33 bytes), time= 2590 seconds
no anomalies in 215 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 16 gigabytes (2^34 bytes), time= 5174 seconds
no anomalies in 226 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 32 gigabytes (2^35 bytes), time= 10336 seconds
no anomalies in 235 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 64 gigabytes (2^36 bytes), time= 20670 seconds
no anomalies in 247 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 128 gigabytes (2^37 bytes), time= 41333 seconds
no anomalies in 258 test result(s)
rng=RNG_stdin, seed=0x5a46a561
length= 256 gigabytes (2^38 bytes), time= 82622 seconds
Test Name Raw Processed Evaluation
BCFN(2+0,13-0,T) R= +7.3 p = 2.0e-3 unusual
[Low4/32]Gap-16:B R= -4.6 p =1-7.6e-4 unusual
...and 265 test result(s) without anomalies
rng=RNG_stdin, seed=0x5a46a561
length= 267.750 gigabytes (2^38.065 bytes), time= 86413 seconds
Test Name Raw Processed Evaluation
[Low4/32]Gap-16:B R= -4.4 p =1-1.0e-3 unusual
...and 266 test result(s) without anomalies
With the output from random_receiver.py being:
############################
Duration (s): 86413.78157377243
Packets Rx: 196913992
Bytes Rx (B): 287494428320